Uji Chi Square

Apa Kabar Semua ...

Pada kesempatan kali ini saya akan menjelaskan Artikel tentang Uji Chi Square.

Semoga Artikel saya selalu bermanfaat dan menjadi referensi bagi kalian semua para pembaca.

Terimakasih atas kunjungannya, Selamat membaca ...

Uji Chi Square

PENDAHULUAN

   Pengujian dengan menggunakan Chi-Square diterapkan pada kasus dimana akan diuji apakah frekuensi data yang diamati (frekuensi/data observasi) sama atau tidak dengan frekuensi harapan atau frekuensi secara teoritis. Chi-Square disebut juga dengan Kai Kuadrat. Chi Square adalah salah satu jenis uji komparatif yang dilakukan pada dua variabel, di mana skala data kedua variabel adalah nominal. Apabila dari 2 variabel, ada 1 variabel dengan skala nominal maka dilakukan uji chi square dengan merujuk bahwa harus digunakan uji pada derajat yang terendah.


   Nilai dari frekuensi observasi adalah suatu nilai yang diperoleh dari hasil percobaan sedangkan nilai frekuensi harapan (ekspektasi) adalah nilai yang diperoleh dari hasil perhitungan secara teoritis. Untuk selanjutnya, frekuensi obervasi dinotasikan dengan (o) dan frekuensi harapan dinotasikan dengan (e).

   Nilai X2 adalah nilai kuadrat karena itu nilai X2 selalu positif. Bentuk distribusi χ² tergantung dari derajat kebebasan. Untuk lebih jelasnya, akan diilustrasikan cara membaca tabel X2 yang ada pada Lampiran. Misalkan diberikan derajat kebebasan db = 5 dengan . Dengan a = 0,01 membaca tabel X2 pada lampiran, diperoleh nilai X2 = 15,086.

   Dalam pengujian Chi square, hal yang dapat diuji antara lain adalah uji independensi, uji Goodness of Fit, uji homogenitas, dan uji varians. Dalam buku ini, yang dibahas adalah mengenai uji independesi dan uji goodness of fit.


   Uji independensi adalah uji untuk menentukan apakah antara variabel independen dan variabel dependennya terdapat perbedaan (hubungan) yang nyata atau tidak. Misalnya, kita ingin mengamati apakah terdapat perbedaan yang nyata antara pendidikan dengan pekerjaan, maka uji yang tepat dilakukan adalah uji independensi dengan Chi square.

   Uji Goodness of Fit (kecocokan) adalah uji untuk menentukan apakah sebuah populasi mengikuti distribusi tertentu atau tidak. Misalnya, kita ingin mengetahui apakah populasi yang diamati berrdistribusi normal atau tidak, atau mungkin populasi yang diamati ternyata berdistribusi poisson, dan seterusnya. Sehingga uji yang digunakan adalah uji Goodness of Fit dengan Chi square.

Uji Independensi

   Seperti yang telah disebutkan di pendahuluan, Uji independensi adalah uji yang dilakukan untuk mengetahui apakah terdapat hubungan antara variabel independen dengan variabel dependen. Sebelum membahas contoh soal, alangkah baiknya kita mengetahui terlebih dahulu syarat uji independensi.

Syarat Uji independensi

   Ada beberapa syarat yang harus dipenuhi jika akan melakukan pengujian dengan Chi Square. Berikut dijelaskan syarat-syarat yang harus dipenuhi, diantaranya:

• Tidak ada cell dengan nilai frekuensi kenyataan atau disebut juga Actual Count ( Fo) sebesar 0 (Nol).
• Apabila bentuk tabel kontingensi 2 x 2 , maka tidak boleh ada 1 cell saja yang memiliki frekuensi harapan atau disebut juga expected count (“Fn ”) kurang dari 5.
• Apabila bentuk tabel lebih dari 2 x 2 , misal 2 x 3 , maka jumlah cell dengan frekuensi harapan yang kurang dari 5 tidak boleh lebih dari 20%.

Jenis Uji Chi Square

   Ada beberapa rumus yang digunakan untuk menyelesaikan suatu pengujian Chi Square. Seperti rumus koreksi yates, Fisher Exact Test, dan Pearson Chi Square. Berikut rincian penggunaan rumus-rumusnya. 

• Jika tabel kontingensi berbentuk , maka rumus yang digunakan adalah “koreksi yates”.
• Apabila tabel kontingensi , tetapi cell dengan frekuensi harapan kurang dari 5, maka rumus harus diganti dengan rumus “Fisher Exact Test”.
• Rumus untuk tabel kontingensi lebih dari , rumus yang digunakan adalah “Pearson Chi-Square”,

KOREKSI YATES

FISHER EXACT TEST

PEARSON CHI SQUARE

PROSEDUR UJI CHI SQUARE.

Contoh 2.

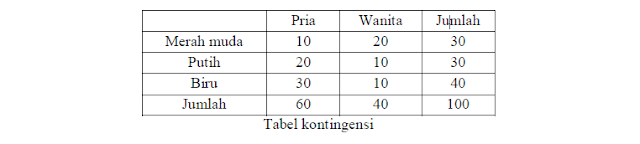
   Dari 100 karyawan di PT XYZ, 60 adalah pria dan 40 adalah wanita. Dari 60 orang pria ternyata 10 menyukai pakaian warna merah muda, 20 menyukai warna putih dan 30 menyukai warna biru. Sedangkan dari 40 orang karyawan wanita, 20 menyukai warna merah muda, 10 menyukai warna putih dan 10 menyukai warna biru. Dengan tingkat kepercayaan 95% apakah antara pemilihan warna dengan jenis kelamin berbeda secara nyata?

Penyelesaian.

   Sebelum melakukan pengujian hipotesis, terlebih dahulu dibuat tabel kontingensi berdasarkan informasi yang ada di contoh 4.

   Berdasarkan Tabel 8, dapat dilihat bahwa ukuran dari tabel kontingensi tersebut adalah . Artinya terdapar 3 baris dan 2 kolom. Selanjutnya, kita akan melakukan prosedur pengujian hipotesis.

CONTOH 3.

   Diketahui data 60 responden. Dari ke 60 responden tersebut, ada responden yang mempunyai pekerjaan 1 dan 2 serta pendidikan 1 dan 2. Misalkan pekerjaan 1 adalah pegawai negeri dan pekerjaan 2 adalah pegawai swasta. Serta pendidikan 1 adalah lulusan SMA, pendidikan 2 adalah lulusan sarjana, dan pekerjaan 3 adalah lulusan magister. Data dari ke 60 responden tersebut, disajikan dalam Tabel berikut.

Penyelesaian:

   Goodness of Fit Test (Uji kecocokan) Uji kecocokan atau goodness of fit test menentukan apakah sebuah populasi mengikuti distribusi tertentu. Chi-Square Goodness of Fit dapat digunakan ketika bertemu dengan kondisi sebagai berikut:

•  Metode sample yang digunakan adalah simple random sampling
• Variabel yang digunakan adalah kategorikal 
• Nilai yang diharapkan pada sampel yang diobservasi minimal 5 dalam setiap level variabel

Contoh 4.

Berikut diberikan data hasil survey 1000 perokok terhadap 5 merek rokok yang mereka pilih.

Latihan Soal

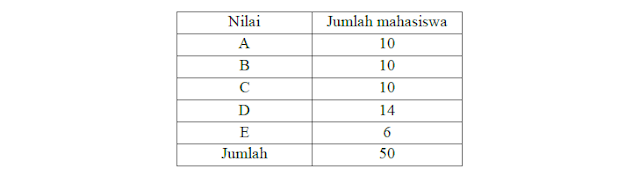
1. Sebuah perguruan tinggi swasta yakin bahwa untuk mata kuliah statistika, persentasi mahasiswa yang akan mendapat nilai A adalah 10%, nilai B adalah 20%, nilai C adalah 40%, nilai D 20% dan yang mendapat nilai E sebesar 10%. Dari hasil ujian akhir sebanyak 50 mahasiswa didapat hasil sebagai berikut :

   Dengan melihat hasil tersebut, benarkah pernyataan dosen perguruan tinggi swasta tersebut pada taraf nyata 5%?

2. Berikut ini dilakukan penelitian untuk mengetahui apakah terdapat hubungan antara status dengan pengeluaran per bulan. Dari 200 mahasiswa 100 mengaku punya pacar, dan sisanya jomblo. Dari 100 mahasiswa yang punya pacar , 83 mengaku pengeluaran besar, 5 pengeluaran sedang dan 12 pengeluaran tetap rendah. Sedangkan dari mahasiswa yang jomblo, 87 mengaku pengeluaran tinggi, 11 pengeluaran sedang dan 2 pengeluaran rendah. Ujilah pada alpha 10% apakah terdapat hubungan antara status dengan tingkat pengeluaran mahasiswa?

7. Seorang administrator rumah sakit, ingin menguji hipotesis nol bahwa penerimaan

pasien gawat darurat mengikuti distribusi Poisson dengan . Misalkan selama periode 90 hari, jumlah penerimaan pasien Gawat darurat disajikan dalam tabel berikut.

8. Sebuah survei berminat menyelidiki determinasi orang dalam mencegah factor-faktor risiko penyakit jantung koroner. Setiap subjek dari sampel berukuran 200 orang diminta menyatakan sikapnya terhadap sebuah pertanyaan kuesioner sebagai berikut “ apakah anda yakin dapat menghindari makanan berkolesterol tinggi” dengan hasil 70 orang sangat yakin, 50 orang yakin, 45 orang ragu-ragu, dan 35 orang sangat ragu-ragu. Dapatkah kita menarik kesimpulan berdasarkan data tersebut, bahwa keempat sikap yang berbeda menyebar merata di dalam populasi asal sampel?