SUMMARY STATISTIK: Analisis of Varians (ANOVA)

Apa Kabar Semua ...

Pada kesempatan kali ini saya akan menjelaskan Artikel tentang Analisis of Varians (ANOVA).

Semoga Artikel saya selalu bermanfaat dan menjadi referensi bagi kalian semua para pembaca.

Terimakasih atas kunjunganny, Selamat membaca ...

Analisis of Varians (ANOVA)

PENDAHULUAN

Kita ketahui bahwa kumpulan hasil pengamatan mengenai sesuatu hal, skor hasil belajar siswa, berat bayi yang baru lahir misalnya, nilai datanya bervariasi dari yang satu dengan yang lain. Karena adanya variasi ini untuk sekumpulan data, telah dihitung alat ukurnya, yaitu varians. Varians bersama rata-rata juga telah banyak digunakan untuk membuat kesimpulan mengenai populasi, baik secara deskriptif maupun induktif melalui penaksiran dan pengujian hipotesis mengenai parameter.

Varians untuk sekumpulan data melukiskan derajat perbedaan atau variasi nilai data individu yang ada dalam kelompok data tersebut. Secara umum varians dapat digolongkan ke dalam varians sistematik dan varians standar. Varians sistematik adalah pengukuran karena adanya pengaruh yang menyebabkan skor atau nilai data lebih condong ke satu jalur tertentu dibandingkan ke jalur lain.

Salah satu jenis varians sistematik dalam kumpulan data hasil penelitian adalah varians antar kelompok atau disebut juga varians eksperimental. Varians ini menggambarkan adanya perbedaan antara kelompok-kelompok hasil pengukuran. Dengan demikian varians ini terjadi karena adanya perbedaan antara kelompok-kelompok individu. Jika uji kesamaan dua rata-rata atau uji t digunakan untuk mencari perbedaan atau persamaan dua rata-rata, maka uji beberapa rata-rata digunakan untuk mencari perbedaan atau persamaaan beberapa rata-rata. Uji ini disebut dengan nama analysis of variance (ANOVA).

Pada prakteknya, uji t dapat juga digunakan untuk menguji beberapa rata-rata secara bertahap. Misalnya ada tiga rata-rata yaitu: I, II, dan III. Agar uji t dapat dipakai maka mula-mula dicari I dengan II, kemudian I dengan III, dan akhirnya II dengan III. Dengan demikian kita tiga kali menggunakan uji t. Namun, pengujian lebih tepat apabila menggunakan beberapa rata-rata. Sebab:

Sebelum uji kesamaan beberapa rata-rata dilakukan, maka persyaratannya haruslah dipenuhi terlebih dahulu. Persyaratan uji beberapa rata-rata sama halnya dengan uji kesamaan dua rata-rata yaitu data dipilih secara acak, data berdistribusi nomal, dan datanya homogen.

PENGERTIAN ANOVA

Analisis of Varians (ANOVA) adalah teknik analisis statistik yang dikembangkan dan diperkenalkan pertama kali oleh Sir R. A Fisher. ANOVA dapat juga dipahami sebagai perluasan dari uji-t sehingga penggunaannya tidak terbatas pada pengujian perbedaan dua buah rata-rata populasi, namun dapat juga untuk menguji perbedaan tiga buah rata-rata populasi atau lebih sekaligus.

Jika kita menguji hipotesis nol bahwa rata-rata dua buah kelompok tidak berbeda, teknik ANOVA dan uji-t (uji dua pihak) akan menghasilkan kesimpulan yang sama; keduanya akan menolak atau menerima hipotesis nol. Dalam hal ini, statistik F pada derajat kebebasan 1 dan n-k akan sama dengan kuadrat dari statistik t.

ANOVA digunakan untuk menguji perbedaan antara sejumlah rata-rata populasi dengan cara membandingkan variansinya. Pembilang pada rumus variansi tidak lain adalah jumlah kuadrat skor simpangan dari rata-ratanya, yang secara sederhana dapat ditulis sebagai Σ(Xi - u ) . Istilah jumlah kuadrat skor simpangan sering disebut jumlah kuadrat (sum of squares). Jika jumlah kuadrat tersebut dibagi dengan n atau n - 1 maka akan diperoleh rata-rata kuadrat yang tidak lain dari variansi suatu distribusi. Rumus untuk menentukan varians sampel yaitu,

Seandainya kita mempunyai suatu populasi yang memiliki variansi 02 dan rata-rata u . Dari populasi tersebut misalkan diambil tiga buah sampel secara independent, masing-masing dengan n1,n2 dan n3 . Dari setiap sampel tersebut dapat ditentukan rata-rata dan variansinya, sehingga akan diperoleh tiga buah rata-rata dan variansi sampel yang masing-masing merupakan statistik (penaksir) yang tidak bias bagi parameternya. Dikatakan demikian, karena dalam jumlah sampel yang tak hingga, rata-rata dari rata-rata sampel akan sama dengan rata-rata populasi (u ) dan rata-rata dari variansi sampel juga akan sama dengan variansi populasi (o2 ).

c. setiap kali kita menggunakan uji t, maka akan terjadi kesalahan atau penyimpangan sebesar (1-a )k , di mana = sekian kali menggunakan uji t. Seandainya kita 3 kali menggunakan uji t,dengan ,maka akan

Alasan penggunaan ANOVA

Uji hipotesis dengan ANOVA digunakan, setidaknya karena beberapa alasan berikut:

Memudahkan analisa atas beberapa kelompok sampel yang berbeda dengan resiko kesalahan terkecil.
Mengetahui signifikansi perbedaan rata-rata (μ) antara kelompok sampel yang satu dengan yang lain. Bisa jadi, meskipun secara numeris bedanya besar, namun berdasarkan analisa ANOVA, perbedaan tersebut TIDAK SIGNIFIKAN sehingga perbedaan μ bisa diabaikan. Sebaliknya, bisa jadi secara numeris bedanya kecil, namun berdasarkan analisa ANOVA, perbedaan tersebut SIGNIFIKAN, sehingga minimal ada satu μ yang berbeda dan perbedaan μ antar kelompok sampel tidak boleh diabaikan.

Pada dasarnya ANOVA dibedakan menjadi dua bagian, yaitu ANOVA satu jalur (one way ANOVA) dan ANOVA dua jalur (two way ANOVA). Pada ANOVA satu jalur dibahas tentang ukuran sampel sama dan ukuran sampel tidak sama. sedangkan untuk ANOVA dua jalur, dibahas mengenai ANOVA tanpa interaksi serta ANOVA dengan interaksi.

ANOVA SATU JALUR

Dinamakan analisis varians satu jalur, karena analisisnya menggunakan varians dan data hasil pengamatan merupakan pengaruh satu faktor. Dari tiap populasi secara independen kita ambil sebuah sampel acak, berukuran n1 dari populasi kesatu, n2 dari populasi kedua dan seterusnya berukuran nk dari populasi ke k. Data sampel akan dinyatakan dengan Yij yang berarti data ke-j dalam sampel yang diambil dari populasi ke-i.

ANOVA satu jalur yaitu analisis yang melibatkan hanya satu peubah bebas. Secara rinci, ANOVA satu jalur digunakan dalam suatu penelitian yang memiliki ciri-ciri berikut:

1. Melibatkan hanya satu peubah bebas dengan dua kategori atau lebih yang dipilih dan ditentukan oleh peneliti secara tidak acak. Kategori yang dipilih disebut tidak acak karena peneliti tidak bermaksud menggeneralisasikan hasilnya ke kategori lain di luar yang diteliti pada peubah itu. Sebagai contoh, peubah jenis kelamin hanya terdiri atas dua ketgori (pria-wanita), atau peneliti hendak membandingkan keberhasilan antara Metode A, B, dan C dalam meningkatkan semangat belajar tanpa bermaksud menggeneralisasikan ke metode lain di luar ketiga metode tersebut.

2. Perbedaan antara kategori atau tingkatan pada peubah bebas dapat bersifat kualitatif atau kuantitatif.

3. Setiap subjek merupakan anggota dari hanya satu kelompok pada peubah bebas, dan dipilih secara acak dari populasi tertentu.

Tujuan dari uji ANOVA satu jalur adalah untuk membandingkan lebih dari dua rata-rata. Sedangkan gunanya untuk menguji kemampuan generalisasi. Maksudnya dari signifikansi hasil penelitian. Jika terbukti berbeda, berarti kedua sampel tersebut dapat digeneralisasikan (data sampel dianggap dapat mewakili populasi). ANOVA satu jalur dapat melihat perbandingan lebih dari dua kelompok data.

ANOVA pengembangan atau penjabaran lebih lanjut dari uji-t. Uji-t atau uji-z hanya dapat melihat perbandingan dua kelompok data saja. Sedangkan ANOVA satu jalur lebih dari dua kelompok data. Contoh: Perbedaan prestasi belajar statistika antara mahasiswa tugas belajar ( x1), izin belajar ( x2) dan umum (x3 ).

ANOVA lebih dikenal dengan uji-F (Fisher Test), sedangkan arti variasi atau varian itu asalnya dari pengertian konsep “Mean Square” atau kuadrat rerata (KR).

Rumusnya:

PROSEDUR PENGUJIAN HIPOTESIS

Sebelum ANOVA dihitung, asumsikan bahwa data dipilih secara random, berdistribusi normal, dan variannya homogen.

Contoh Soal dan Pembahasan.

Pada contoh soal ANOVA, disini diberikan dua contoh untuk sampel yang berukuran sama dan untuk sampel yang ukurannya berbeda. Proses pengerjaan pengujian hipotesisnya pada hakikatnya sama, yang berbeda hanyalah pada penentuan derajat kebebasannya. untuk lebih jelasnya, silahkan dipelajari dua contoh berikut ini.

CONTOH 1. (Sampel berukuran sama)

Dari 5 tablet obat sakit kepala yang berbeda diberikan kepada 25 orang yang sakit kepala (pusing). Setelah beberapa jam, obat itu dapat mengurangi rasa sakit. Ke-25 orang tersebut dibagi secara acak kedalam 5 kelompok dan masing-masing diberi satu jenis obat. Berikut data lamanya minum obat tersebut dengan berkurangnya rasa sakit. Berikut datanya.

Dengan menggunakan taraf nyata 5%, Ujilah pendapat yang mengatakan bahwa rata-rata kelima obat tersebut memberikan efek yang sama.

Penyelesaian.

Karena Fo > Ftabel maka Ho ditolak. Artinya ada perbedaan rata-rata lamanya pengaruh obat dalam mengurangi rasa sakit kepala setiap orang dengan tingkat keyakinan 95%.

CONTOH 2. (Sampel berukuran tidak sama).

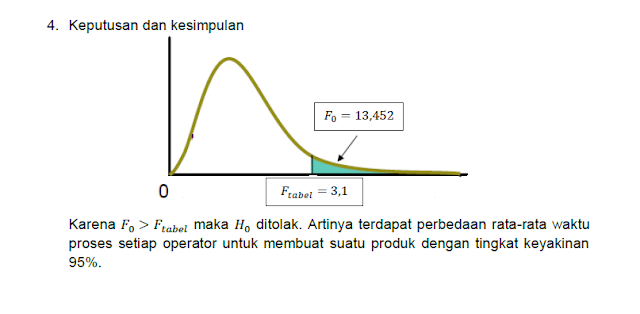
Untuk menguji apakah operator yang berbeda akan mempengaruhi waktu proses (dalam menit) untuk membuat suatu produk, dilakukan pengamatan secara bersamaan terhadap 4 orang operator (A, B, C, D). Berikut adalah hasil pengamatannya.

ANOVA DUA JALU

ANOVA dua jalur yaitu pengujian ANOVA yang didasarkan pada pengamatan 2 kriteria. Setiap kriteria dalam pengujian ANOVA mempunyai level. Tujuan dan pengujian ANOVA dua jalur ini adalah untuk mengetahui apakah ada pengaruh dan berbagai kriteria yang diuji terhadap hasil yang diinginkan. Misal, seorang guru menguji apakah ada pengaruh antara jenis media belajar yang digunakan pada tingkat penguasaan siswa terhadap materi. (Hasan, Iqbal. 2010. Pokok-Pokok Materi Statistik 2 (Statistik Inferensial). Jakarta: Bumi Aksara)

Tujuan dari pengujian ANOVA dua jalur adalah untuk mengetahui apakah ada pengaruh dari berbagai kriteria yang diuji terhadap hasil yang diinginkan. (Furqon. 2009. Statistika Terapan untuk Penelitian. Cetakan ketujuh. ALFABETA: Bandung ).

Dengan menggunakan teknik ANOVA dua jalur ini kita dapat membandingkan beberapa rata-rata yang berasal dari beberapa kategori atau kelompok untuk satu variable perlakuan. Bagaimanapun, keuntungan teknik analisis varian ini adalah memungkinkan untuk memperluas analisis pada situasi dimana hal-hal yang sedang diukur dipengaruhi oleh dua atau lebih variable. (Hasan, Iqbal. 2003. Pokok-Pokok Materi Statistik 2 (Statistik Inferensial). Jakarta: Bumi Aksara).

ANOVA dua jalur ini digunakan bila sumber keragaman yang terjadi tidak hanya karena satu faktor (perlakuan). Faktor lain yang mungkin menjadi sumber keragaman respon juga harus diperhatikan. Faktor lain ini bisa berupa perlakuan lain yang sudah terkondisikan. Pertimbangan memasukkan faktor kedua sebagai sumber keragaman ini perlu bila faktor itu dikelompokkan, sehingga keragaman antar kelompok sangat besar, tetapi kecil dalam kelompoknya sendiri. Pengujian ANOVA dua jalur mempunyai beberapa asumsi diantaranya:

1. Populasi yang diuji berdistribusi normal,

2. Varians atau ragam dan populasi yang diuji sama,

3. Sampel tidak berhubungan satu dengan yang lain.

ANOVA Dua jalur tanpa interaksi

Pengujian klasifikasi dua jalur tanpa nteraksi merupakan pengujian hipotesis tiga rata-rata atau lebih dengan dua faktor yang berpengaruh dan interaksi antara kedua faktor tersebut dtiadakan. tujuan dari pengujian hipotesis ANOVA dua jalur adalah untuk mengetahui apakah ada pengaryh dan berbagai kriteria yang diuji terhadap hasil yang diinginkan.

ANOVA Dua Jalur dengan Interaksi

Pengujian klasifikasi dua jalur dengan interaksi merupakan pengujian beda tiga rata-rata atau lebih dengan dua faktor yang berpengaruh dan pengaruh interaksi antara kedua faktor tersebut diperhitungkan. Pada dasarnya, pengujian hipotesis ANOVA dua jalur dengan interaksi sama seperti ANOVA dua jalur tanpa interaksi. yang berbeda hanya pada Tabel ANOVAnya. Berikut diberikan tabel ANOVA untuk ANOVA dua jalur dengan interaksi.

Contoh Soal dan Pembahasan

Suatu percobaan diadakan untuk meneliti pengaruh suhu dan jenis tungku terhadap umur sejenis suku cadang tertentu yang diuji. Empat jenis tungku dan tiga taraf suhu dipakai dalam percobaan tersebut. Duapuluh empat buah suku cadang dibagi secara acak, dua pada tiap kombinasi perlakuan, dan hasilnya dicatat sebagai berikut.