Apa Kabar Semua ...
Pada kesempatan kali ini saya akan menjelaskan Artikel tentang Kolerasi Dan Regresi Linier Berganda.
Semoga Artikel saya selalu bermanfaat dan menjadi referensi bagi kalian semua para pembaca.
Terimakasih atas kunjungannya, Selamat membaca ...
KORELASI DAN REGRESI LINIER BERGANDA
REGRESI SEDERHANA
Menurut Abdurahman (2011), secara umum ada dua macam hubungan antara dua variabel atau lebih, yaitu bentuk hubungan dan keeratan hubungan. Analisis regresi digunakan untuk mengetahui bentuk hubungan antara dua variabel atau lebih, terutama untuk menelusuri pola hubungan yang modelnya belum diketahui dengan sempurna, atau untuk mengetahui bagaimana variasi dari beberapa variabel independen mempengaruhi variabel dependen dalam suatu fenomena yang kompleks. Jika X1, X2, .. Xi adalah variabel-variabel independen dan Y adalah variabel dependen, maka terdapat hubungan fungsional antara X dan Y , dimana variasi dari akan diiringi pula oleh variasi dari Y. Secara matematika hubungan di atas dapat dijabarkan sebagai berikut: Y = F(X1, X2, ... Xi, e) , dimana Y adalah variabel dependen, X adalah variabel independen dan e adalah variabel residu (disturbance term).
Akumulasi berbagai faktor dapat menyebabkan suatu persoalan dalam kehidupan di sekitar kita tiap harinya. Sebuah kejaadian dipicu oleh berbagai peristiwa sebelumnya, sehingga untuk menduganya diperlukan sebuah persamaan matematik yang bisa merangkum berbagai faktor tersebut. Apabila sebuah kejadian Y akan terikat oleh berbagai faktor X yang bebas, karena itu bila regresi linear dipakai untuk menduga Y variabel tak bebas atas X variabel bebas yang cuma satu maka ada persamaan matematik yang dibuat untuk memecahkan persamaan tersebut, yaitu persamaan regresi linear berganda (Hiariey, 2009).
Prediksi perubahan variabel dependent (Y) akan menjadi lebih baik apabila dimasukkan lebih dari satu variabel independent dalam persamaan liniernya (X1, X2, Xn ). Hubungan antara lebih dari satu variabel independen dengan satu variabel dependen inilah yang dibicarakan dalam analisis regresi linier berganda. Hubungan antara banyak variabel inilah yang sesungguhnya terjadi dalam dunia nyata, karena sebenarnya kebanyakan hubungan antar variabel dalam ilmu soisal merupakan hubungan statistikal, artinya bahwa perubahan nilai Y tidak mutlak hanya dipengaruhi oleh satu nilai X tertentu tetapi dipengaruhi oleh banyak nilai X.
Model regresi linier berganda melibatkan lebih dari satu variabel bebas. Modelnya
TAKSIRAN KOEFISIEN REGRESI PARSIAL
Dari hasil Metode Kuadrat Terkecil didapatkan persamaan normal :
Ada 10 rumah tangga yang merupakan sampel acak dari suatu penelitian. Antara lain ditanyakan tentang banyaknya konsumsi atas komoditi tertentu, harga komoditi dan pendapatan.
Permintaan terhadap komoditi tersebut untuk keperluan konsumsi (Y) akan dipengaruhi oleh harga ( X1) dan pendapatan (X2 ). Berikut hasil penelitiannya
Buatlah persamaan regresinya.
Penyelesaian:
Dengan menggunakan metode kuadrat terkecil dengan matriks. Berarti menentukan matriks A , vektor g dan vektor b .
Dari pembahasan diatas, diketahui rumus untuk matriks A adalah sebagai berikut.
PENGUJIAN HIPOTESIS KOEFISIEN REGRESI PARSIAL
Pengujian hipotesis dilakukan jika terdapat seseorang yang mempunyai pendapat atau argumen dan ingin dibuktikan kebenarannya. Misalnya seseorang beranggapan bahwa lamanya belajar mahasiswa dan IQ akan mempengaruhi terhadap IP yang diperoleh pada setiap semesternya. Hal ini dapat dibuktikan kebenarannya dengan melakukan pengujian hipotesis. Untuk lebih jelasnya mengenai prosedur pengujian hipotesis tentang regresi linier berganda, dapat diilustrasikan menggunakan skema berikut.
Langkah-langkah pengujian hipotesis:

KORELASI SEDERHANA
Apabila kita mempunyai tiga variabel Y, X1, X2, maka kita dapat menentukan hubungan atau korelasi sederhana antara X1 dan Y,X2 dan Y , serta X1 dan X2.
korelasi dan digambarkan dengan rumus berikut :
KOEFISIEN KORELASI LINEAR BERGANDA (KKLB)
UJI REGRESI LINIER DENGAN SPSS
Tujuan
Analisis regresi linier sederhana digunakan untuk menguji pengaruh satu variabel bebas terhadap variabel terikat.
Syarat Uji Regresi Linier Sederhana
- Data haruslah valid dan reliabel dan berasal dari data primer.
- Data juga harus lolos uji asumsi dasar yang mencakup uji normalitas dan uji linieritas.
Dasar Pengambilan Keputusan
Pengambilan keputusan dalam uji regresi linier sederhana dapat mengaju pada dual hal, yakni:
1. Membandingkan nilai signifikansi dengan nilai probabilitas 0.05
- Jika nilai signifikansi <0.05, artinya variabel X berpengaruh terhadap variabel Y.
- Jika nilai signifikansi >0.05, artinya variabel X tidak berpengaruh terhadap variabel Y.
2. Membandingkan nilai t-hitung dengan t-tabel
- Jika nilai t_hitung>t_tabel, artinya variabel X berpengaruh terhadap variabel Y.
- Jika nilai t_hitung<t_tabel, artinya variabel X tidak berpengaruh terhadap variabel Y.
Asumsi-asumsi diatas harus dipahami terlebih dahuku sebelum memulai melakukan uji regresi linier sederhana menggunakan perangkat lunak SPSS.
Penyelesaian menggunakan SPSS
Langkah pertama:
Buka aplikasi SPSS dengan cara Klik windows-programs-IBM SPSS Statistics- IBM SPSS Statistics 24. Berikut adalah tampilan dari halaman muka dari software SPSS versi 24:
Langkah Kedua:
Mendefinisikan data, caranya dengan:
- Klik Tab Variabel View
- Klik pada Cell di baris pertama kolom Name, kemudian tuliskan X
- Klik pada Cell di baris kedua kolom Name, kemudian tuliskan Y
- Klik pada Cell di baris pertama kolom Label, kemudian tuliskan Harga Produk
- Klik pada Cell di baris kedua kolom Label, kemudian tuliskan Loyalitas Pelanggan
- Klik Tab Data View
- Input data yang akan dianalisis ke dalam program SPSS
Langkah Ketiga:
Menganalisis data menggunakan modul analyze pada software SPSS dengan cara:
- Klik Modul Analyze-Regression-Linier
- Pindahkan variabel Harga Produk pada tab Independent(s)
- Pindahkan variabel Loyalitas Pelanggan pada tab Dependen
- Klik OK
Pada tahapan ini akan menghasilkan output seperti tampilan dibawah ini:
Langkah Keempat:
Melakukan interpretasi hasil output uji regresi linier sederhana menggunakan SPSS.
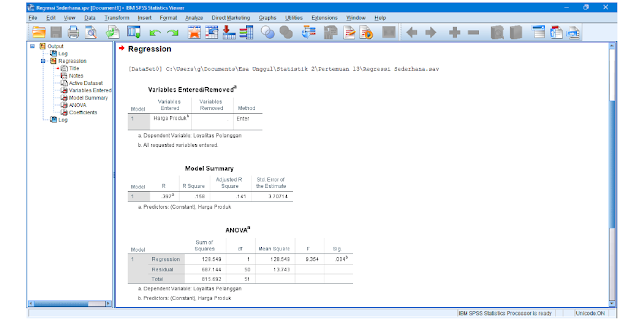
Output SPSS dan Penjelasannya:
Pada tabel diatas menjelaskan tentang variabel yang dimasukkan serta metode yang digunakan. Dalam hal ini variabel yang dimasukkan adalah variabel Harga Produk sebagai variabel independen dan Loyalitas Pelanggan sebagai variabel dependen dan metode yang digunakan adalah metode Enter.
Pada tabel diatas menjelaskan tentang besarnya nikai korelasi atau hubungan (R) yaitu sebesar 0.463. Dari output tersebut kdiperoleh koefisien determinasi (R Square) sebesar 0.215 yang mengandung pengertian bahwa pengaruh variabel bebas ( Dalam kasus ini adalah Harga Produk) terhadap variabel terikat/dependen (Dalam studi kasus ini adalah Loyalitas Pelanggan) adalah sebesar 21.5%.
Pada tabel diatas menjelaskan tentang apakah model regresi dapat dipakai untuk memprediksi variabel independen terhadap variabel dependen. Dari output tersebut diketahui bahwa nilai F hitung sebesar 13.951 dengan tingkat signifikansi sebesar 0.000<0.05, maka dapat dikatakan bahwa model regresi dapat dipakai untuk memprediksi pengaruh variabel Harga Produk (X) terhadap variabel Loyalitas Pelanggan (Y).
Pada tabel diatas menjelaskan tentang diketahuinya nilai constant (a) sebesar 9.481 sedangal nilai Harga Produk (X) sebesar 0.438, sehingga persamaan nya dapat dituliskan sebagai berikut:
Y= a+bX
Y= 9.481 + 0.438X
Persamaan tersebut dapat diterjemahkan sebagai berikut:
- Konstanta sebesar 9.481, mengandung arti bahwa nilai konsisten variabel Harga Produk adalah sebesar 9.481.
- koefisien regresi X sebesar 0.438 menyatakan bahwa setiap penambahan 1% nilai Harga Produk, maka nilai Loyalitas Pelanggan bertambah sebesar 0.438. Koefisien regresi tersebut bernilai positif, sehingga dapat dikatakan bahwa arah pengaruh variabel X terhadap Y adalah positif.
Pengambilan Keputusan dalam Uji Regresi Linier Sederhana
1. Berdasarkan nilai signifikansi.- Dari tabel di Coefficients, diperoleh nilai signifikansi sebesar 0.000<0.005, sehingga dapat disimpulkan bahwa variabel Harga Produk (X) berpengaruh terhadap variabel Loyalitas Pelanggan (Y).
1. Berdasarkan nilai t.
- Diketahui nilai t_hitung sebesar 3.735 > t_tabel sebesar 2.008, sehingga dapat disimpulkan bahwa variabel Harga Produk (X) berpengaruh terhadap variabel Loyalitas Pelanggan (Y).
Lampiran 1: Cara mencari nilai t_tabel
Lampiran 2: Kurva Uji Regresi Linier Sederhana
Analisis Regresi Linier Berganda Dengan SPSS
Konsep dasar analisis regresi linier berganda :
- Analisis regresi berganda bertujuan untuk mengetahui ada atau tidaknya pengaruh dua atau lebih variabel bebas/independen (X) terhadap variabel terikat/dependen.
- Uji t bertujuan untuk mengetahui ada atau tidaknya pengaruh parsial (Sendirian) yang diberikan variabel bebas (X) terhadap variabel terikat (Y)
- Uji F bertujuan untuk mengetahui ada atau tidaknya pengaruh simultan (bersama-sama) yang diberikan variabel bebas (X) terhadap variabel terikat (Y).
- Koefisien determinasi berfungsi untuk mengetahui berapa persen pengaruh yang diberikan variabel X secara simultan terhadap variabel Y
Perumusan Hipotesis
H1= Terdapat Pengaruh Design Produk (X1) terhadap Loyalitas Pelanggan (Y)
H2= Terdapat Pengaruh Kualitas Produk (X2) terhadap Loyalitas Pelanggan (Y)
H3= H1= Terdapat Pengaruh Design Produk (X1) dan Kualitas Produk (X2) secara simultan terhadap Loyalitas Pelanggan (Y).
Tingkat kepercayaan atau confidence level 95%
Dasar Pengambilan Keputusan
1. Berdasarkan Uji t.
- Jika nilai sig < 0.05 atau t_hitung > t_tabel maka terdapat pengaruh variabel X terhadap variabel Y.
- Jika nikai sig > 0.05 atau t_hitung < t_tabel maka tidak terdapat pengaruh variabel X terhadap variabel Y. t_tabel = t {(a/2)/(n-k-1)} = t (0.025/9)= 2.262
2. Berdasarkan Uji F.
- Jika nilaj sig<0.05 atau F_hitung>F_tabel maka terdapat pengaruh variabel X secara simultan terhadap variabel Y.
- Jika nilaj sig>0.05 atau F_hitung<F_tabel maka tidak terdapat pengaruh variabel X secara simultan terhadap variabel Y. F_tabel = F (k/n-k) = F (2/10) = 4.10
Penyelesaian menggunakan SPSS
Langkah pertama:
Buka aplikasi SPSS dengan cara windows-programs-IBM SPSS Statistics- IBM SPSS Statistics 24.
Langkah Kedua:
Mendefinisikan data, caranya dengan:
- Klik Tab variabel view
- Klik pada Cell di baris pertama kolom Name, kemudian tuliskan X1
- Klik pada Cell di baris kedua kolom Name, kemudian tuliskan X2
- Klik pada Cell di baris ketiga kolom Name, kemudian tuliskan Y
- Klik pada Cell di baris pertama kolom Label, kemudian tuliskan Design Produk
- Klik pada Cell di baris kedua kolom Label, kemudian tuliskan Kualitas Produk
- Klik pada Cell di baris ketiga kolom Label, kemudian tuliskan Loyalitas Pelanggan
- Klik Tab Data View
- Input data yang akan dianalisis ke dalam program SPSS
Langkah Ketiga:
Menganalisis data menggunakan modul analyze pada software SPSS dengan cara:
- Klik Modul Analyze-Regression-Linier
- Pindahkan variabel Harga Produk pada tab Independent(s)
- Pindahkan variabel Loyalitas Pelanggan pada tab Dependent
- Klik OK
Pada tahapan ini akan menghasilkan output seperti tampilan dibawah ini:
Langkah Keempat:
Melakukan interpretasi hasil output uji regresi linier berganda menggunakan SPSS.
Pengujian Hipotesis dengan Uji t
A. Pengujian Hipotesis Pertama (H1)
Diketahui nilai signifikansi untuk pengaruh X1 terhadap Y adalah sebesar 0.347>0.05 dan nilai t hitung 0.992<t_tabel 2.262, sehingga dapat disimpulkan bahwa H1 ditolak yang berarti tidak terdapat pengaruh X1 terhadap Y.
B. Pengujian Hipotesis Kedua (H2)
Diketahui nilai signifikansi untuk pengaruh X2 adalah sebesar 0.007<0.05 dan nilai t_hitung sebesar 3.441 > t_tabel 2.262, sehingga dapat disimpulkan bahwa H2 diterima yang berarti bahwa terdapat pengaruh X2 terhadap Y.
C. Pengujian Hipotesis Ketiga (H3)
Berdasarkan output diatas diketahui nilai signifikansi untuk pengaruh X1 dan X2 secara simultan terhadap Y adalah sebesar 0.000<0.05 dan nilai F_hitung sebesar 23.978 > F_tabel sebesar 4.10, sehingga dapat disimpulkan bahwa H3 diterima yang berarti bahwa terdapat pengaruh X1 dan X2 secara simultan terhadap Y.
D. Interpretasi Koefisien Determinasi Dari Tabel Output Model Summary
Berdasarkan output diatas diketahui nilai R Square sebesar 0.842, hal ini mengandung arti bahwa pengaruh variabel X1 dan X2 secara simultan terhadap variabel Y adalah sebesar 84.2%.
Lampiran 3: Cara mencari nilai F_tabel
Contoh: - Probability = tingkat kesalahan (a) = 0.05
- Jumlah variabel bebas = 1
- Jumlah sampel (n) = 3
- deg_freedom1 = dk pembilang = Jumlah variabel bebas = k = 1
- deg_freedom2 = dk penyebut (n-k-1) = 3-1-1 = 1
Maka formulanya adalah = FINV(0.05,1,1)
Nilai F tabel yang diperoleh = 161,45
Lampiran 4: Kurva Uji Regresi Linier Berganda